The quarterback rating was something that always intrigued me. To have a formula to compare players based on a combination of stats is great. But, I’ve always had problems with what the NFL uses to rate quarterbacks. I first wanted to simplify the QB Rating equation, but I could never get it right, (This guy did) so I had to move on from that. Then I thought what does the QB rating actually mean? Philip Rivers lead the league with a QB rating of 105.5 this year, how good is that? How much better is that than the 10th QB on the list, Matt Cassel at 89.4? And more importantly, what does that 16.1 point difference in rating actually mean. Most sports statistics mean something. In baseball, ERA is the amount of earned runs a pitcher gives up in 9 innings, hockey has points for goals and assists, and in basketball they keep track of points per game. All are great ways to compare players and all have meaning behind the stats.
First, I did some searching online and discovered that the QB rating was created in 1973 by an executive at the Pro Football Hall of fame, Don Smith. Smith’s formula compares a quarterback’s performance based on the total of all quarterback performances in the past 10 years. In the formula that Smith created, he separates completion percentage, passing yardage, TDs and interceptions and awards 1 point for an average game and 2 points for a record breaking game and zero for a terrible game. Smith weighted each category and averaged out the numbers and bam you get the QB Rating. With the top QB rating being 158.3 and the lowest of course is 0, average was supposed to be 66.7. The average for the past 10 years was 80.1.
What if you could compare the quarterback’s stats to their team’s chances to winning the game? This makes the most sense, they touch the ball more than any other player on the team. And why not, they get all the credit when the team wins and all the blame when they lose? So I took every quarterback’s stats from every game the last ten years and put a winning percentage to each category. For example if a quarterback doesn’t throw an interception in the game his team's chances of winning is 66.11%. If a QB throws 2 TDs, he wins 58% of the time. A completion percentage of 40% only wins 18.8% of the time. I graphed each number found the best line to fit the graph.
I did this for each category and kept the stats that had the strongest correlation to winning. I found that completion %, total TDs, total turnovers, yards/play and sacks all had extremely strong graphs. Surprisingly total passing yards didn’t, the graph was all over the place.
The only stat that I was keeping the same from the old equation was completion percentage. All the others were tweaked a bit. It makes more sense especially with today’s football to include things like rushing yards, rushing TDs and fumbles. Even true pocket passers, QB sneak it into the endzone every once in a while. To prove my point, Peyton Manning has 17 career rushing TDs. And when all is said and done Peyton running the ball in for a score gets the same result as him throwing it in, so shouldn’t his rating benefit the same?
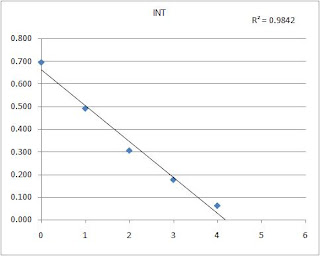
For each category I have a linear equation with an R2 of over .97. For all people that aren’t math nerds, the simplest way I can explain it is, R2 is, when using linear lines, a number that shows how strong a line fits with to a set of data points. The number 1.00 means the line fits perfect and 0 the not fitting at all. TDs and turnovers have the strongest correlation with a .999 and the other categories not too far behind, yards/play .97, sacks .98 and completion percent at .98.
After I got the equation for each category I did a weighted average and got your Kosmo Winning Percentage (Why wouldn’t I name my formula after myself?). Now this equation is uglier than the old version, but it uses stats that have a connection to what you play for, winning the game. Another way to say it is, this number shows which QB put their team in best position to win games.
Using the KWP this year’s top passer was not Phillip Rivers, it was Drew Brees with a number of .640. Now one may look at this number and think that it seems odd or small for a rating the top QB of the year. But the QB is just one of several pieces of the puzzle to win the game. There are other factors like the Saints 23rd ranked defense or 28th ranked rush offense, both decreasing their chances of winning games. And the reason why they won 8 games instead of the 10 predicted.
Just because the KWP is higher than the opposing QB doesn’t always mean you will win the game. Just take this year’s Super Bowl for example. Kurt Warner’s numbers put the Cardinals in a better position to win with a KWP of .647 compared to Big Ben’s .567, but The Steelers defense made big plays, specifically James Harrison 100 yard TD.
With this new rating there is no cap or floor, it goes slightly outside of the 1.000-.000 scale of winning percentage. The best game ever played by a QB, Johnny Unitas 11/12/67, got a KWP of 1.062 and the worst game ever played Ryan Leaf 9/20/98, got a KWP of -0.010. It didn’t like that there were 47 “perfect” games for QBs, with some games way more impressive than others.
Football is evolving; the game isn’t close to what it was back in 1973. I think it’s time for a new way to rate quarterbacks and this is the way to do it.
I listed my formula and some new rankings below. This season’s KWP, Top Careers, Stand-Out Seasons, “Perfect” Games and “Zero” games.



I am up for ideas on how to improve the formula or other suggestions.





11 comments:
A good sanity check is Football OUtsiders' DYAR, and your rankings for last season look pretty good compared to FO's DYAR. I'd say that KWP looks pretty solid so far.
http://www.footballoutsiders.com/stats/qb
Lovely. What are your thoughts on Flacco's relatively low ranking? And what font did you use to write up the formula (or is your handwriting really that awesomely consistent)?
Crane, Flacco isn't high on the list because he was average this year in most categories. Below average in TDs and Yrds/Play. Flacco won becuase he defense made plays and the Raven had a strong run game.
The Font was something in paint named Chiller.
Well Kosmo, I certainly give you credit for your effort. This looks like a lot of work. But I am still quite confused. But I don't really understand the current QB rating system either.
did you look at Yards-per-Attempt at all as a driver for wins? i would think that YPA could be more valuable than straight completion %. that's just off the top of my head though.
ZZZZZZZ... Ironic that Kosmo is the same guy who in January replied to one of Dr. G's astute comments, "Dr. G writes too much, doesn't he know how blogs work. I read half of his comments and stopped caring." Unlike folks with a life, I guess Kosmo gets excited by numbers. I'm no mathematician, but I'm guessing that any equation that includes the value K must equal ZERO....
I didn't use yrd/att, it's more of yards/play. Rush yrd + Pass yrd - sck yrd per attempt. It has a stronger correlation to winning then yrd/att. Completion percentage has an amazing strong factor if a team wins. A R2 of .983
Here are my thoughts and reactions (not necessarily in any particular order):
You suggest early on that the qb rating system should actually mean something. While you are to be commended for relating a qb rating to a winning probability, you don't actually show how KWP correlates with winning percent. For example, what does a KWP of 0.62 mean versus a KWP of 0.52? A discussion of what the #s mean would be helpful.
You show examples of certain statistics (TDs thrown in a game versus winning percentage, for example) correlated with winning percentage, but you don't sow how all the pieces fit together correlate with winning percentage.
Also, you suggest you looked at the past 10 years. Completions per attempt and interceptions per attempt have changed materially over the past 10 years (completions per attempt has been increasing, interceptions per attempt has been decreasing). I expect these trends to continue. How does your formula take this into account?
I like the fact that you've "modernized" the formula by including sacks, total TDs, fumbles, and rushing attempts and yards. Unfortunately, it has made the formula a little more complicated, so, in terms of anyone actually adopting it, its probably not going to happen.
Also, in the formula, do you actually mean fumbles or fumbles lost? I think you mean fumbles lost. I've found that the likelihood of retaining or losing a fumble is about equal (it's awfully close to 0.50), so you could "improve" the formula by substituting fumbles * 0.50 as opposed to actually using fumbles lost (since that is random).
One of my biggest criticisms of the current qb rating formula is that it is confusing, at best. Yours would be confusing to most "normal" people, and would only be "appreciated" by stat/numbers geeks like you and me.
One of my other big criticisms of the current formula is the fact that it includes TDs (and only passing TDs at that). While your formula improves on the current one by also including rushing TDs, what difference does it make whether the QB runs it in or the RB runs it in? As you know, my formula does not include ANY TDs. Either include ALL TDs, or none. Don't penalize quarterbacks who play on teams that have good running backs (see Troy Aikman). And, you can extend this argument even further. Why not include ALL scoring, such as field goals? Especially if your formula relates a QB rating to a winning percentage, then I would think you'd want to somehow reflect rushing TDs as well as field goals.
That all being said, it's a good first attempt, and, I'm sure you'll be refining it over time. In addition to my own site (http://newqbrating.blogspot.com), there are several others independently developing (or, have developed) alternatives to the current formula. You may want to check out footballoutsiders.com, pro-football-reference.com and, in particular, advancednflstats.com. There are some really smart guys out there doing some really cool stuff. I wish the NFL would pay attention to all of us, who I'm sure collectively can come up with something simple, elegant and meaningful.
Cheers,
Kiran
I always appreciate good insight on rating QBs. That said, I've got a couple of comments that I think would help your system.
It's almost impossible to separate out cause and effect in football. If I told you that the Cowboys were 100-2 when Emmitt Smith ran 20 times in a game, your immediate reaction would probably be "well the Cowboys would run the ball when they're winning, so duh" and not "they should run Emmitt every play of every game to guarantee victory!" That's because the causation arrow runs both ways -- 20 carries is both an indicator that your team is winning (which is highly correlated with wins) and that your RB is very good (which is always correlated with wins). It's easy to see that when I use that example; it's less obvious but no less accurate to say that passing completions are both a cause and effect of winning.
Teams that are winning will throw safe, conservative passes. Teams that are losing will throw risky passes. So just because completion percentage is correlated with winning does *not* mean completion percentage *causes* winning. And I think, to a lesser extent, the same is true of INTs.
I like your ideas of using fumbles, and I'm working on something similar. Incorporating rushing data for QBs is tricky.
I've got a bunch of thoughts on ranking QBs here:
http://www.pro-football-reference.com/blog/?p=540
http://www.pro-football-reference.com/blog/?p=481
http://www.pro-football-reference.com/blog/?p=547
I don't feel the QB rating should be related to the Teams Won/Lost record, no more than a pitchers ERA relates to Teams win/loss. Way too many intangibles to develop any rating that crosses all generations of time.
QB ratings can be negative. Example no completions and multiple INTs
Post a Comment